Working Paper Series ——— 2/2021

The Effects of Minimum Wage Increases in the Czech Republic 

www.cnb.cz

 

 

 

 

The Working Paper Series of the Czech National Bank (CNB) is intended to disseminate the results of the CNB’s research projects as well as the other research activities of both the staff of the CNB and collaborating outside contributors, including invited speakers. The Series aims to present original research contributions relevant to central banks. It is refereed internationally. The referee process is managed by the CNB Economic Research Division. The working papers are circulated to stimulate discussion. The views expressed are those of the authors and do not necessarily reflect the official views of the CNB.

 

Distributed by the Czech National Bank, available at www.cnb.cz 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Reviewed by:                  Katalin Bodnár (European Central Bank)

                                      Jan Babecký (Czech National Bank)

Project Coordinator:  Michal Franta

Issued by:                       © Czech National Bank, August 2021 

 

The Effects of Minimum Wage Increases in the Czech Republic

Jakub Grossmann^*

Abstract

This paper analyzes employment effects of four minimum wage increases implemented in the Czech Republic during 2012–2017, which cumulatively increased the national minimum wage by 37 percent. We analyze outcomes at the level of firm-occupation-county-specific job cells and apply an intensity-treatment estimator similar to that of Machin et al. (2003). Our preferred specifications suggest that minimum wage increases led to higher wages for low-paid workers and did not have significant impacts on their employment.

Abstrakt

Tento clánek mˇ eˇˇrí dopady náru°stu° minimální mzdy na zamestnanost nízkovýdˇ elkových zamˇ est-ˇ nancu° v Ceské republice v letech 2012–2017, kdy kumulativní náru°st minimální mzdyˇ           cinil 37ˇ procent. Pro urcení kauzálního vztahu využíváme identifikaˇ cní strategii podobnou té, jež byla po-ˇ užita napˇríklad v Machin, Manning a Rahman (2003). Výsledky meˇˇríme na úrovni pracovních bunek, které jsou tvoˇ ˇreny kombinací firmy, povolání a regionu, ve kterých zamestnanci pracují.ˇ Naše výsledky naznacují, že zkoumané náru°sty minimální mzdy mírnˇ e navýšily mzdy nízkový-ˇ delkových pracovníku° a zároveˇ n nemˇ ely výraznˇ ejší dopad na zmˇ enu zamˇ estnanosti.ˇ

 JEL Codes:         J31, J38, J68.

 Keywords:        Czech Republic, job cells, minimum wage, treatment intensity.

*Jakub Grossmann, Czech National Bank and CERGE-EI, a joint workplace of Charles University and the Eco-nomics Institute of the Czech Academy of Sciences, Politickych veznu 7, 111 21, Prague 1, Czech 

Republic. Email: jakub.grossmann@cerge-ei.cz.

The author would like to express his gratitude to the Ministry of Labor and Social Affairs for its consent to use the SES data and to the TREXIMA company, which provided the calculations. The author is grateful to Štepánˇ Jurajda for his supportive guidance, and Vladimír Smolka, Mariola Pytlíková, Nikolas Mittag, Jan Babecký, Katalin Bodnár, as well as participants at the Workshop on Regional Economics at Ifo Institute in Dresden, the TU Dresden research seminar, and the Empirical Microeconometrics Workshop in Bolzano for useful comments. All errors and omissions remain the fault of the author.

1. Introduction

A large literature studies the ramifications of minimum wages, including its central effect on employment. Most of this work concludes that minimum wage increases have minor to no disemployment effects.^[1] A problem with extending this predominantly US-based research to European countries is that the European minimum wage legislation is typically applied at the national level, which limits the use of region-based difference-in-differences identification strategies. Two types of approaches have been devised to allow identification of national minimum wage effects. First, the bunching estimator compares the number of jobs created above the level of an increased minimum wage level with the number of jobs destroyed just below that level (e.g. Meyer and Wise, 1983; Harasztosi and Lindner, 2019; Cengiz et al., 2019), assuming that the wage distribution would remain the same in the absence of a minimum wage increase. Second, the treatment-intensity estimator relies on variations in treatment exposure to national minimum wages typically generated by the pre-existing share of workers whose wages are below the minimum wage level set for the next year. This strategy, applied at the firm and/or establishment level, allows researchers to compare firms that would have to increase their wage bills to varying degrees due to a minimum wage increase (introduction) in order to retain all their workers (Machin et al., 2003; Eriksson and Pytlikova, 2004; Harasztosi and Lindner, 2019).

In this paper, we employ both these strategies and are the first to apply the treatment-intensity approach at the level of job cells, defined as the combination of employee’s occupation and employer’s location. We study the impacts of four increases in the national minimum wage (NMW) in the Czech Republic implemented during 2012-2017. These increases followed a period of 7 years in which the NMW was not increased despite a concurrent cumulative growth of 16% in mean nominal wages in the economy (The Czech Statistical Office, 2019).^[2] Starting at EUR 320^[3] (32% of the average wage) at the beginning of 2013, these changes amount to a total increase of 37.5% increase in the national minimum wage which reached EUR 440 in 2017 (46% of the average wage). The highest annual increase occurred in 2017, when the NMW increased by 11%. We consider these increases both separately and together, as one significant increase in the NMW.

We start our analysis by applying the treatment-intensity estimator at the firm level (as applied by Harasztosi and Lindner, 2019, for example). This means, we measure the treatment exposure to a NMW increase by the share of employees of a firm who are currently paid a wage that is below the minimum wage level set in the next period (we refer to this measure as “the Share”) and by the proportion of an employers’ total wage bill that corresponds to the sum of wages that would have to be increased so that all current employees are paid at least the minimum wage in next period (“the Gap” measure). A potential weakness of this strategy is, first, that minimum wage increases could be timed to correspond to demand shocks in industries that employ a large share of low-wage workers, i.e. that an unobserved demand shock at the firm level could make the minimum wage endogenous. Second, since the share of workers paid below a future NMW in the average firm was around 3%^[4] in 2012, such a strategy confuses the effects of NMW on low-wage employment with the evolution of employment at wages well above the NMW level, which is unlikely to be causally affected by the NMW. Indeed, some applications of the treatment-intensity approach focus on specific establishments characterized by a high exposure to NMW increases and homogenous labor composition (e.g. Machin et al., 2003 who study care homes). This, however, limits the generalizeability of the results.

In the second step of our analysis, we therefore employ treatment intensity variation at the jobcell level, where job cells are groups of workers in the same firm, in the same location and with the same occupation, and we study only low-wage job cells. This allows us to exploit variation in exposure to NMW increases at the level of homogenous groups of low-wage workers, i.e., we do not mix the NMW effects on employment of low- and high-wage employees. The strategy also allows us to control for firm-level evolution of employment by conditioning on firm FE. We supplement the employment analysis of NMW effects at the job-cell level by asking whether NMW increases affected job-cell worker turnover and employment structure in terms of education, gender, or firmspecific worker tenure.^[5]

Third, we apply a bunching estimator. Assuming that there would be no change in real wage distribution in the absence of NMW increases, we compare the number of jobs created above a new NMW level with the number of jobs destroyed below the new NMW level. The real wage distribution from a period preceding a NMW increase is used as a counterfactual. We examine employment dynamics in the region of +/- EUR 100 (CZK 2,500) around a new NMW level, i.e. approximately 70-130% of the NMW level in 2013.

Our analysis relies on the Czech Structure of Earnings Survey (SES), which has several advantages for conducting a study on NMW effects.^[6] The SES is a large panel that covers almost 4,000 firms, providing detailed information about all employees working in the firms surveyed. The SES covers approximately 1.5 million employees each year (out of about 3.5 million salaried employees in the Czech private employment sector). This allows us to observe a large number of homogenous job cells and to exploit significant variations in treatment exposure to NMW increases across these cells. The SES also allows us to study changes in hours worked in addition to changes in employment.

Figure 1 shows that each of the four NMW increases did result in a shift in wage distribution.^[7]Individual graphs show wage distribution in years before and after each NMW increase; the only exception is Figure 1 (a) which shows wage distribution for 2012 and 2014 because the NMW increase was implemented in the middle of 2013. Black horizontal lines denote the initial levels of the NMW and red lines indicate NMW levels after each increase.

Our firm-level analysis produces mixed results. We find a significantly negative employment effect associated with the 2013 NMW increase, but positive employment effects associated with the NMW increases in 2015 and 2016. The employment elasticity with respect to minimum wage associated with the 2013 increase is -0.154^[8] (the estimated coefficient is almost 25%). One possible explanation is that employers had already considered possible future NMW increases and adjusted employment accordingly. It could also be that our exposure measures correlate with the employment trends of high-wage workers within a firm. It is worth stressing that another factor may be Figure 1: Changes in Wage Frequency Distributions

                         (a) NMW Increase in 2013                                                  (b) NMW Increase in 2015

(c) NMW Increase in 2016

(d) NMW increase in 2017

behind such a large estimate. We analyze the NMW increase in 2013 using data from 2012 and 2014. In addition, it is possible that the estimated coefficient also captures changes in employment that were not caused by the NMW increase. The size of the firm-level estimate is large compared to previous work. For example, Eriksson and Pytlikova (2004) found in one specification that a NMW increase in the Czech Republic in 2000 resulted in a 14% decrease in employment. Our estimates show that subsequent NMW increases in 2015 and 2016 had the opposite (i.e. s positive) effect on employment, in both cases amounting to an increase in employment of approximately 16% (the employment elasticity wrt. NMW are 0.03 and 0.08, respectively). We do not find any statistically significant employment effects associated with the 2017 NMW increase.

Our job-cell results are more consistent and in line with the existing literature, compared to the firmlevel results. The estimated coefficients do not switch from negative to positive and vice versa over the years. We find negative employment effects for the 2013 NMW increase only. However, this effect is economically small and below the level of estimates appearing in the recent literature. The NMW increase in 2013 led to an 11% drop in employment for job cells in which all employees were paid less than the NMW (corresponding to an elasticity of -0.066), which is small in comparison to previous research. We also find a small negative and statistically significant effect on employment in 2016 in one specification. Next, we focus on selected job cells. First, we analyze 5 of the most affected occupations separately.^[9] We find no negative employment effects using these job cells. Second, we focus on job cells in accommodation and restaurants. Our preferred specification does not show any negative effects on employment. Third, NMW increases do not show negative effects on employment in the manufacturing industry, except for the NMW increase in 2013 when analyzed separately.

In line with our treatment-intensity analysis, the bunching-based estimates indicate that employment changes induced by the NMW increases were negligible. Some 4% of jobs around the minimum wage threshold were destroyed in 2017, representing the most extreme case. We also find positive employment effects associated with the 2013 and 2015 increases. However, the bunching estimates are sensitive to the upper and lower bounds selected, which determine the area of wage distribution where employment changes are measured.

We supplement our job-cell analysis by inspecting additional effects of NMW increases. We find that the NMW increases during 2013-2017 did not affect: i) hours worked, ii) turnover rates or iii) educational and gender composition of job cells. Furthermore, by estimating the employment effects on specific parts of the job-cell employment distribution^[10], we address the possible correlation between labor demand shocks and the employment evolution of exposed job cells. Our findings suggest that labor demand shocks did not affect our results at the job-cell level. We also estimate the effects of a hypothetical situation in which a sizable NMW increase is implemented. We combine the individual NMW increases during 2012–2017 and treat them as one large NMW hike. Our estimates suggest that such a considerable increase would not have a negative effect on employment.

To better understand the sources of discrepancies between estimates at the firm and job cell levels, we ask how well the firm-level exposure measure predicts employment changes for both low-paid workers and for high-paid employees. Our results find no statistically significant relationship, i.e. increases in the minimum wage did not cause decreases in the employment of low-paid employees. This contradicts our firm-level estimates. A closer look at the estimated coefficients for control variables shows that they differ significantly in the two subsamples. This finding suggests that the firm-level aggregated characteristics fail to sufficiently control for the specific characteristics of low-paid employees and likely correlate with the firm-level minimum wage exposure. Therefore, we do not find our firm-level estimates credible and our preferred results are those estimated at the job-cell level. One of the lessons learned is that the treatment-intensity strategy should be applied on homogenous groups of employees to estimate the effects of minimum wage increases; otherwise, the estimated effects may be biased.

This paper relates in several ways to the existing literature on the minimum wage. First, we contribute to the work on the employment effects of minimum wage increases. Similar to recent EU analyses, we find that the increases in the NMW we study have little or no negative effect on employment. Second, our paper contributes to the part of the literature that applies a treatmentintensity estimator to estimate the employment effects of NMW increases. Often, this approach is the only possible means of identifying the causal effects of nation-wide minimum wage increases. This type of research is usually carried out at the firm level (e.g., as in Harasztosi and Lindner 2019, and Eriksson and Pytlikova 2004, who use the SES data), or researchers use occupation-specific organizational units (as in Machin et al. 2003 who analyzed employment patterns in the care-homes industry during the introduction of a NMW in the UK). The major advantage of using the SES or similar data is that such data-sets include the characteristics of a large number of firms and their employees. However, the firms surveyed are large heterogenous organizational units that may employ only a small fraction of workers exposed to a NMW increase.^[11] Therefore, measuring the exposure to a NMW increase by the share of affected employees in firms is likely to be inaccurate. Moreover, this approach mixes the employment trends of low- and high-paid workers. The other alternative used in the literature is to focus on specific occupational units that group together employees with similar wages and characteristics. Therefore, it is possible to precisely zoom in on low-paid employees and study changes in their employment. The drawback is that it is difficult to collect such data-sets. Furthermore, the estimated effects of an NMW increase are not generalizable. In this paper, we focus on firm-occupation-county-specific job cells and combine the benefits of the two approaches. Using the SES data provides a large number of observations, making it possible to focus on specific labor-market segments, i.e. to target subgroups of employees that are likely to be affected by a NMW increase and to compare job cells that are similar. Job cells are small homogenous units and their characteristics derived from information on individuals are more accurate than those of firms. Moreover, when NMW increases are small, the higher variance in exposure at the job-cell level facilitates more precise estimations. We believe that using job cells allows us to compare employees who are in the same part of the wage distribution and have similar individual characteristics, but who differ in terms of exposure to NMW increases. Therefore, we estimate the true effects of NMW increases whilst the firm-level analysis also includes the effects on employees who are paid well above the minimum wage. Third, we contribute to the literature on the effects of NMW increases in the Czech Republic. Only a few papers have studied the effects of minimum wage changes in the Czech Republic ( Eriksson and Pytlikova 2004; Fialová and Mysíková 2009; Duspivová et al. 2013). Eriksson and Pytlikova (2004) study relatively large increases – varying from 11.1% to 35.8% – in the minimum wage in the Czech Republic during 1999-2002. Using the Czech Structure of Earnings Survey (SES) data, they estimate the effects of NMW increases on wages and employment of low-paid employees at the firm level. They follow the approach used in Card (1992) and construct two variables which measure exposure to NMW increases. Their findings suggest that legislative changes had a positive effect on wages and a small negative effect on employment in some specifications, especially for small firms.

This paper proceeds as follows. Section 2 presents the institutional context. Section 3 describes the data. Section 4 presents our units of interest - job cells. Section 5 shows the methods we apply. Section 6 presents the employment analysis. Section 7 presents wage effects. Section 8 shows the bunching-based estimates. Section 9 concludes.

2. Institutional Context

The existence of a minimum wage is anchored in the Czech Labor Code. The minimum wage has been changed 20 times over the last 25 years (Ministry of Labour and Social Affairs, 2018). The majority of changes occurred during 1998-2007, when the minimum wage more than tripled to EUR 320 (CZK 8,000 per month). This level remained stable until 2013. Since then, the minimum wage has been adjusted every year except in 2014.^[12] The percentage increases with monthly minimum wage levels in brackets are 6.25% (EUR 340 / CZK 8,500), 8.2% (EUR 368 / CZK 9,200), 7.6% (EUR 396 / CZK 9,900) and 11.1% (EUR 440/ CZK 11,000) in August 2013, January 2015, January 2016, and January 2017 respectively. The minimum wage in the Czech Republic is established by Act no. 262/2006 Sb. (Labor Code) and the minimum wage levels are set by Government Decrees.

Plans for increasing the minimum wage level are usually discussed openly, and include input from employee and employers representatives. However, the Government is ultimately responsible for deciding the minimum wage levels in the Czech Republic. A Government Decree becomes binding by upon its entry into the Legal Code. Minimum wage Government Decrees are usually published in the Legal Code during the fall, and become effective as of January 1st, allowing employers time to prepare, to some extent, for the wage increases.^[13]

Figure 2 shows the evolution of the monthly minimum wage in the Czech Republic together with the minimum wage to average wage and the minimum wage to median wage ratios. Red bars indicate the timing of the minimum wage changes. The minimum wage to average wage ratio varies from approximately 0.3 to 0.42 during the period observed; the rates are similar to those in neighboring countries in the region (OECD, 2018).

Figure 2: Minimum Wage Evolution

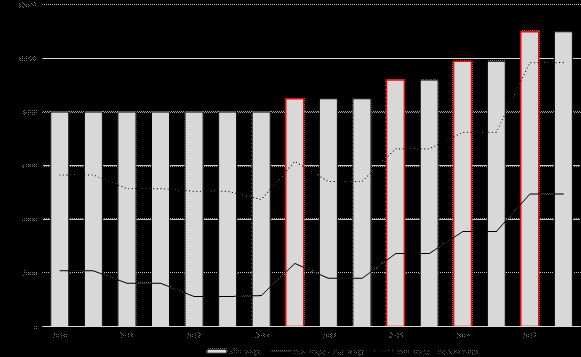
The Czech Republic is a central European post-communist country whose economic activities are distributed unevenly across regions. This diversity results in the minimum wage setting being most effective in certain industry, occupation and regional-specific clusters. The simple (unweighted) average wage in NUTS-4 regions in the Czech Republic is EUR 1,150 (CZK 28,761) with a standard deviation of 113.3 (2,833); the average industrial wage (according to 19 CZ-NACE groups) is EUR 1,114 (CZK 27,857) with a standard deviation of 359.8 (8,919); the average wage of CZ-ISCO major groups is EUR 1,041 (CZK 26,027) with a standard deviation of 340 (8,492) (The Czech Statistical Office, 2017). The lowest wages are traditionally in accommodation and food services, and in administrative and support service industries. Occupations with the lowest wages in the Czech Republic are mainly elementary occupations, and service and sales workers with an average monthly wage of EUR 619 (CZK 15,466) and EUR 670 (CZK 16,755) respectively in 2016. According to the Ministry of Labor and Social affairs (2018), the average unemployment rate across 77 NUTS4 counties was 3.8% with a standard deviation of 1.45 at the end of 2017.

3. Data

We use information on private-sector employees from the Czech Structure of Earnings Survey for 2012-2017.^[14] The data include an unbalanced panel of firms with repeated cross-section observations regarding all workers employed by each firm.^[15] We work with annual data, i.e. we use aggregated data that were reported in each quarter of the year. We use data for 2012 and 2014 to analyze the first increase in NMW, as the increase took effect in the middle of 2013. For the rest of the increases, which occurred in January of each year, we use data on the two years either side of each NMW increase. Firm-level data provide information about firms´ location (NUTS4 classification), a 4-digit NACE industry code, and the presence of a collective agreement. Data on employees include gender, age, place of work (NUTS4), hours worked, salary, 4-digit ISCO occupation, education, and tenure in the job. The number of observations in the annual surveys vary from 1.23 to 1.31 million per year during the period studied. After dropping observations with missing values and keeping only full-time workers, we are left with approximately 95% of the original data in each year.

4. Job Cells

Our main units of interest are firm-occupation-county-specific job cells. Job cells are groups of employees with similar skills and wages, and we argue that they are more homogenous than firms in terms of employment dynamics. There are 3,655 firms and 51,977 job cells in our data for 2012. The higher number of job-cell observations allows us to zoom in on the bottom segment of the job-cell wage distribution (that of low-paid workers). Assuming that changes in the employment of high-paid and low-paid employees differ, focusing solely on low-paid job cells brings us closer to satisfying the identifying assumption of the same employment evolution in organizational units which are and are not affected by the NMW increase.

We generate job-cell characteristics from the individual characteristics of employees who belong to the same job cell. Most importantly, we create a log(cell wage) as the mean of the individual log(monthly wages) and log cell employment for each year. Similarly, we generate shares of females, Czech nationals, average age, tenure, and their squared counterparts.

5. Methods

Unlike in US-based research, we cannot apply region-based difference-in-differences identification strategies. Therefore, we use the treatment-intensity estimator applied in, e.g., Machin et al. (2003). This approach compares organizational units with different treatment exposures to a NMW increase, to estimate the causal effects of NMW increases on changes in employment and wages. The underlying identification assumption is that affected and non-affected firms / job cells would follow the same employment evolution in the absence of NMW increases.^[16] The treatment exposure is typically measured by the share of employees who are paid below the NMW level set for the year ahead. Below, we define two measures representing the exposure to NMW changes, which we subsequently use in regressions in which changes in wages and employment are on the LHS and the exposure measures are on the RHS of our regression equations. This approach allows us to identify which of the changes in employment and wages are caused by increases in the NMW.

We define the indicator for worker i who is paid in period t below a new NMW level set in period t+1:

(

                                                                                  1       if NMWt+1 > monthly wagei,t

af fected_i,t =

                                                                                  0     otherwise

We then consider a simple share of workers paid below a new NMW level (extensive margin) and call it the Share,

_?af fectedi,j,c,o,t i

                                                                       Share_j,c,o,t =                                                                   (1)

^Nj,c,o,t

where a subscript j stands for firms, c county, o occupation and N is the total number of workers within a specific firm / job cell. The share measure equals the share of workers below the new NMW and captures the extent to which a firm / job cell is exposed to an upcoming change in the NMW. However, the Share measure does not give us information on the intensity of the effects. Therefore, we construct another variable called Gap which measures the size of this exposure (intensive margin) at the firm/job-cell level. ^[17] This measure also reflects the size of job cells, this being larger for job cells with more workers provided that the values of the Share variable are similar.

i

                                                                      Gapj,c,o,t =                                                                  (2)

?wij i

Where the w_t^min₊₁ variable is a NMW level expressed in terms of the monthly wage and the w_ij variable is the average monthly wage computed as the total money paid to a worker during the period observed, divided by the number of months an employee has worked at a firm. See the Appendix for more details about the construction of the monthly wage. The Gap variable measures the proportion of employers’ wage bills that must be increased so that all workers are paid at least the NMW level set in next period.

More than 21,000 employees are directly affected by the 2013 NMW increase in our dataset in 2012, corresponding to less than 2% of employees (unweighted). These workers must either be paid an increased wage or be laid off. The share of employees affected by the subsequent increase was 0.85%. The share was growing since then, accounting for 2.09% in 2015, and 2.37% in 2016. Mean distances between the monthly wages of affected workers and the new NMW level in the next period vary at around EUR 23-36 (CZK 580-890) across NMW increases. Detailed summary statistics at the individual level can be found in the Appendix, Table B1.^[18]

Our data show that employees affected by changes to the NMW are concentrated in specific occupations and industries. Table B3 in the Appendix summarizes the share of employees affected by NMW increases for each specific ISCO group and for each year. The groups that experienced the highest shares are Elementary Occupations and Service and Sales Workers. In terms of specific industries, the highest share of employees affected are employed in the Hotel and Food Services and Real Estate industries. Detailed statistics can be found in Table B4 in the Appendix.

We also compare the characteristics of the job cells that were/were not affected. We refer to a job cell (firm) as affected “affected” if at least one employee is paid below the NMW level effective in the next period. The jobs cells affected are larger: In 2012, the average size of the job cells affected is 66 employees as against only 18 employees for unaffected job cells. The job cells affected include a significantly higher proportion of females, slightly older employees in some of the years studied, a lower proportion of Czech nationals, and shorter job tenure. The job cells affected have a significantly lower number of hours worked compared to those which were not affected. Not surprisingly, the job cells which were affected include more people with primary and vocational education. Overall summary statistics at the job-cell level are presented in the Appendix, Table B5. Firm level characteristics show similar patterns to the job-cell level; detailed summary statistics can be found in Table B6 of the Appendix.

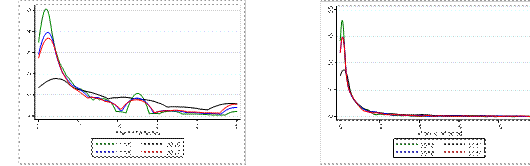
Figures 3a and 3b show the distributions of the Share variable for all job cells and firms affected. Each color represents the distribution for a particular NMW increase. In the case of job cells, the he Share measure has higher variation in the case of job cells; the standard deviations across the years studied vary in the range of 0.21-0.32 and 0.11-0.19 in the case of job cells and firms respectively. The Gap variable is distributed similarly to the Share measure.

6. Employment Effects

To estimate the effects of the NMW increases on employment, we estimate Equation 3

                       ?log(employment)_j,_c,_o,_t =?1+ß1*Share_j,_c,_o,_t-1+ß2*Gap_j,_c,_o,_t-1+?1*X_j,_c,_o,_t-1+?_j,_c,_o,_t                       (3)

where the dependent variable is the change in log(firm / job-cell employment). Our coefficients of interest are ß₁, ß₂ (estimated separately), X are control variables and ? are firm and county two-

Figure 3: Kernel Density of the Share Measure: Firm vs. Job-Cell Level

            (a) Job-Cell Level (Low-Wage Job Cells)                                       (b) Firm Level (All Firms)

way cluster-robust errors. We use the Share and Gap variables to measure NMW exposure. We also weight Eq. 3 by the number of employees in the firms/job cells. The Share coefficient (ß₁) states the average (dis)employment effect for a firm/job cell, where all employees are affected (i.e. paid below the NMW level effective in the next period); the comparison groups are firms/job cells where none of the employees is affected.^[19] Similarly, the Gap coefficient (ß₂) refers to the average (dis)employment effect if employers were compelled to double their wage bills as a consequence of a NMW increase.

We use only firms and job cells that exist in both periods for most of our analysis, i.e. we do not include newly created or destroyed units.^[20] We analyze job cells from the first quartile of the job-cell wage distribution as these units are most likely to be affected by a NMW increase, and they are covariates in terms of their characteristics. Table 1 summarizes the estimated employment effects. Rows represent different econometric specifications. Columns show estimates for three different exposure measures associated with each of the four NMW increases. We focus on the estimated Share coefficients in our interpretation below. In cases where the Gap and the weighted Share estimates are statistically different from zero, the estimated effects have the same signs as the Share estimates. The size of the estimates is similar to our Share estimates in our job-cells specifications.

We first carry out our analysis at the firm level, as this is usually the level used in the literature. Our results are presented on the first line of Table 1. The firm-level results suggest that the NMW increase in 2013 is associated with a negative effect on employment and there are small positive effects on employment in 2015 and 2016. The estimated negative coefficient amounts to almost 25% (employment elasticity^[21] with respect to the minimum wage is -0.154).^[22] One explanation for such a large effect may be that employers had anticipated future increases in minimum wage levels and, thus, adjusted their employment decisions accordingly. Another possible explanation is that the Czech Republic was still experiencing the end of the Great Recession in 2013 so the economic situation was different compared to subsequent years when, during the economic boom, the NMW was increased (The World Bank Group, 2019). To address the possible effect of the economic cycle, we test whether firm-level employment and wages are more procyclical in firms with a higher share of low-paid employees.^[23] We do not find that firms with more low-wage workers have different employment patterns during economic booms and busts.^[24] The full set of results can be found in Tables B15 and B16 in the Appendix. It is also possible that more exposed firms were affected more severely by the negative labor demand shock in 2013.^[25] Finally, it is possible that the firm-level estimates also capture the employment trends of high-wage employees. To address this concern, we estimate the firm-level equation using the employment changes of low- and high-paid employees as separate dependent variables.^[26] Our estimates in Table B13 show that the Share exposure measure at the firm level does not predict employment changes for low- and high-paid employees separately, though the estimates are estimated precisely. A closer inspection reveals that the estimates of control variables significantly differ across these two subsamples. For example, the average industry FE for low-paid employees in 2013 is 0.073, -0.185 for high-paid employees, and the difference is -0.255, which is a sizable effect similar to the firm-level estimate of the Share measure in the same year (see Table 1). This suggests that the application of the treatment intensity estimator on heterogenous groups of employees can lead to biased estimated effects of the minimum wage increases. For this reason, we prefer our job-cell estimates to firm-level estimates.

The results based on our preferred units of interest (job cells) present a different picture. Our estimates suggest that there were little or no negative employment effects. Although we are not able to directly test the identifying assumption of equal employment trends in the absence of NMW increases, we aim to get as close as possible to satisfying this assumption by considering only job cells from the 1st quartile of the job-cell wage distribution. Table 1 shows that there were negative effects on employment only in 2013 and that these effects were negligible. The employment effects in 2013 are comparable for various specifications, amounting to -10.6% in our baseline specification and -13.1% in the specification with firm fixed-effects; the associated employment elasticities with respect to the minimum wage are -0.066 and -0.081 respectively. These effects are small and comparable to previous findings (e.g., Harasztosi and Lindner, 2019, found employment elasticities to be around -0.035). We found consistently statistically significant employment effects only in 2013. Connecting job cells across all years, we are able to estimate the employment effects of the NMW increases, controlling for job-cell fixed-effects. Table B10 presents these estimates. We find a small negative effect on employment which amounts to -5.72% with this specification.

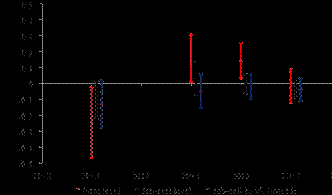
Figure 4 presents the Share estimates for different specifications (the first three rows in Table 1) together with 95% confidence intervals. The horizontal axis indicates the year in which there was an increase in the NMW and the vertical axis shows the size of our coefficient estimates. As recent research argues (Brewer et al., 2019), relevant public policy recommendations should consider not only the failure to reject the null hypothesis but also the range of estimated effects on employment. Figure 4 shows that the firm-level estimates are less precise than their job-cell level counterparts. The absolute values of the point estimates are usually higher in the case of firms. However, they are not statistically different from the job-cell level estimates. Our job-cell level estimates are consistent and economically negligible.

Figure 4: Estimates Comparison - the Share Measure

The employment effects of minimum wage increases are probably the most often studied, however, there are other effects of interest closely related to minimum wage increases.

Specific occupations: Some low-skilled occupations are more likely to be affected by minimum wage increases. Instead of focusing on one specific occupation, we select five occupations with the highest mean values of the Share exposure measure in each year.^[27] The occupations most affected by a NMW increase belong mainly to groups 5 and 9 (Elementary Occupations, and Service and Sales Workers). Our results do not show any negative employment effects during the years studied (Table 1, line “5 most affected occupations”).

Specific industries: We focus on job cells in specific industries, which are likely to be affected by NMW increases. We are interested in the response of the hotel and food service industries to a rise in the NMW.^[28] Surprisingly, we find no statistically significant decrease in employment associated with any of the years studied. Estimates appear in Table 1, line “Accommodation and food services”. We also estimate the employment effects using job cells from the manufacturing industry separately. This is the largest industry in our study, accounting for almost 40% of salaried employees in the Czech Republic. The results presented in Table 1, line “Manufacturing” do not show any disemployment effects, except for the 2013 increase. Our estimate, in terms of size, is similar to the firm-level estimate in the same year, -27% (employment elasticity with respect to minimum wage is -0.106). Similar to the employment effects associated with the NMW increase in 2013 at the firm level, these results are driven by small units (see Table B8).

Destroyed/created job cells^[29]: Considering only job cells that are observable in both periods on either side of the NMW increases in our analysis may overlook systematic closure and/or the creation of job cells. We therefore conduct a robustness exercise, where we assign 0 for employment when a job cell is missing in our data. The results appear on the “0 if missing” line in Table 1. The results indicate that there are negative employment effects mainly associated with the NMW increases in 2013, 2015, and 2016.^[30] Nevertheless, similar to our baseline specification, these estimates are rather small.

110 percent of NMW levels: To account for possible spillovers, we arbitrarily set the NMW levels to 110 percent of their original levels and estimate the employment regressions. We do not find evidence that the NMW increases affected the employment of workers paid above the new NMW levels.

Hours worked: One reasonable concern is that employers may not lay employees off entirely, but may instead reduce their working hours. To investigate this issue, we estimate equations with changes in log hours worked as the dependent variable. The estimates in the row “LHS: Hours worked” in Table 1 shows that such behavior cannot be seen in our data.

Turnover: It is possible that employers replace employees who are paid less than the new NMW with new employees who are paid higher wages. In this case, the employment level could remain the same and the job cell would show higher average cell wages. To explore this issue, we run regressions with turnover as the dependent variable. The results are presented in Table 1. We do not find any systematic evidence that employers replace workers more in job cells in which they are paid below the NMW levels.

Skill substitution: It can also happen that employers who are forced to raise wages engage in skills substitution to mitigate their costs: i.e., replacing low-skilled workers with better-skilled new employees. To investigate this scenario, we run a set of regressions with average educational attainment as the dependent variable (the education category variable ranges from 1 to 6 according to the highest level of educational attainment). We do not find that the substitution of skills occur.

Gender composition: We ask whether employers change the gender composition of job cells as a result of NMW increases. We run regressions with the percentage change in the share of females in job cells as the dependent variable. We do not find that females are systematically replaced by male workers or vice versa. The only significant gender-related results are associated with the NMW increases in 2015 and 2016, and these are economically negligible.

Job-cell fixed-effects: To inspect job-cell-specific effects, we create a panel of job cells for 20122017 and estimate a regression equation with job-cell fixed-effects. Results appear in Table B10.

We see a small negative employment effect of 5.7%. The size of the estimate is in line with our job-cells results. We also observe a positive effect on wage growth of 10.5%.

Unemployment: To address the concern that employment effects in regions with high unemployment rates may be different to those in regions with low unemployment, we control for countyspecific unemployment rates and interact our exposure measures with unemployment rates. We find that the levels of unemployment are important controls only in 2015. Specifically, counties with higher unemployment rates exhibited higher increases in job-cell employment than counties with low unemployment rates. This might suggest that the supply of workers in regions with low unemployment was already depleted due to the economic boom and only firms in counties with high levels of unemployment had opportunity to hire workers. Detailed results can be found in Table B9 in the Appendix.

One large increase in the NMW: The NMW increases we study in the Czech Republic are rather small. To simulate a hypothetical situation in which the minimum wage level is increased significantly, we combine job-cell data from 2012 and 2017^[31], recode our exposure measures, and evaluate one large increase in the NMW. We do not find that this artificial increase in the NMW had any effect on the employment of low-paid employees (see Table B11 for detailed results).

Finally, we would like to stress that we are aware of some aspects for which we are not able to control. One is a wage/benefits substitution. It can happen that some employers reduce employee benefits so they can afford to increase their wages (see e.g. Babecký et al., 2019 who show that employers use non-base wage components to adjust labor costs during economic shocks). Another potential issue can be that employers convert regular employee contracts into self-employment (contractor) contracts. This would show as a disemployment effect in our data, although these workers might not lose income.

7. Wage Effects

The next step in our analysis is to inspect how the 2013-2017 NMW increases affected the wages of low-paid workers. Figures 1a, 1b, 1c, and 1d show visible bunching around new NMW levels, indicating that the NMW increases were binding and, thus, they should have had a positive effect on the wages of low-paid employees. Similarly to the employment effects, we estimate the wage effects of the NMW increases using Equation 4

                    ?log(cellwage)j,c,o,t =?2 +ß3 *Share_j,c,o,t-1 +ß4 *Gap_j,c,o,t-1 +?2 *X_j,c,o,t-1 +?j,c,o,t                     (4)

where the dependent variable is a percentage growth in wages, our coefficients of interest are ß and the regression equations include controls for age, length of employment, gender, share of Czech employees, education category, firm size category, county, industry, and occupation. Table 2 summarizes the results. The columns represent different exposure measures (the Share, the Gap, and the Share weighted by the number of workers employed within units) for each of the NMW increases. The rows represent various levels of our analysis and econometric specifications. The exposure measures capture wage growth better at the job-cell level, and are comparable for all specifications. Our baseline results suggest that NMW increases caused the wages of directly affected employees to be raised by 8%, 9.4%, 2.8%, and 5.5% in 2013, 2015, 2016, and 2017 respectively. Similar to the interpretation of the employment effects, these are the effects for job cells in which all employees are affected and their wages are increased, i.e. none of them is laid off. The growth in wages caused by the NMW increase is slightly smaller when firm fixed effects are included. The highest estimated coefficients across all specifications are associated with the NMW increase in 2015. Table B14 in the Appendix shows the job-cell level ß₃ estimates for different parts of the wage distribution in each year. A comparison between years shows that the estimates are at their highest in 2014 and their lowest in 2015.

Furthermore, we estimate the wage effects on a subsample of the 5 most affected occupations. The estimates are comparable in size to our baseline specification based on all job cells from the 1st quartile of the job-cell wage distribution.

We also present estimates for Accommodation and food services and Manufacturing. There is anecdotal evidence that restaurant employees are often paid only the minimum wage and the rest of their remuneration is paid off the books. If we accept that this is the case, we would observe a significant increase in wages and no negative effects on employment. However, we do not find this pattern in our data. This may be because the Czech SES contains mostly firms with a higher number of employees, and this type of behavior is not practiced.

8. Bunching

The third step in our analysis is to apply the bunching estimator, a common tool applied in the economic literature to estimate the effects of minimum wage changes (e.g. Meyer and Wise, 1983, Harasztosi and Lindner, 2019, or Cengiz et al., 2019).^[32] This approach aims to shed light on the employment changes of workers who are paid around the minimum wage threshold. The bunching estimator allows researchers to clarify how the number of “missing” jobs (compared to a counterfactual wage distribution) below the minimum wage threshold relates to jobs above the threshold added in a new wage distribution. The identifying assumption behind the bunching estimator is that the wage distributions would be the same in the absence of NMW increases. Usually, counterfactual wage distributions are based on wage distributions in the periods prior to changes in NMW or they are artificially created as, for example, in Friedman et al. (2011), who applied a polynomial fit to current period distributions. Upper and lower bounds defining the area of interest are set arbitrarily.

Figures 1a, 1b, 1c, 1d show that the minimum wage changes in the Czech Republic were small and the bunching around the new NMW levels is moderate. We use a real wage distribution, where wages are discounted by the median growth in wages (with a base in 2013), as the rates of inflation were very low during 2012-2017 (varying in the range of 0.3-3.3) and average wages grew much faster than inflation. We set the upper and lower bounds as + /- EUR 100 (CZK 2,500) around the new NMW level, i.e. we capture the employment of everyone whose monthly wage is in a range of approximately 70 - 130 % of the NMW level in 2013. We use the same approach to choose bounds for subsequent increases. This is in line with Harasztosi and Lindner (2019), who use 20%, 35%, and 50% ranges of the new minimum wage.^[33]

Analyzing the 2013 increase, we see that there are approximately 1,300 extra jobs, which means that for every 100 jobs in our range, three new jobs were created. The size and direction of the effect related to the NMW increase in 2015 is almost identical. We observe an increase that amounts to approximately 1,300 jobs (for each 100 jobs 3 new ones were created). In 2016 and 2017 there were very small decreases in employment: 1,260 and 1,440 jobs respectively. This means that for every 100 jobs 3 jobs were destroyed due to the 2016 increase and 4 jobs were destroyed due to the 2017 increase. Our results are similar in magnitude to previous research findings. For example, Harasztosi and Lindner (2019) found that a NMW increase in Hungary in 2001 caused 3 out of 100 workers to lose their jobs.

Our bunching estimates are small (the highest unemployment estimate based on the bunching estimator is approximately three times smaller than the treatment-intensity estimate on the job-cell level in 2013). Also, they do not suggest that the NMW increases we study resulted in consistent disemployment effects.

9. Conclusion

This paper studies four recent increases in the NMW in the Czech Republic from 2013 to 2017. Constructing exposure measures similar to Machin et al. (2003), we examine the effects of the NMW increases on employment and wages at a job-cell level. Compared to previous studies, which work with firm-level observations, we are able to study exposure more precisely for homogenous groups of workers. We show that the application of the treatment intensity estimator on heterogenous groups of people may lead to biased estimates.

Our findings suggest that the NMW increases in our study had positive effects on the wage growth of low-paid workers and had little or no negative effect on employment. In our preferred specification, the employment elasticities with respect to the minimum wage vary between -0.0093 and 0.0017, which are rather small estimates compared to others in the existing literature. Our results are confirmed by several robustness tests.

References

BABECKÝ, J., C. BERSON, L. FADEJEVA, A. LAMO, P. MAROTZKE, F. MARTINS, AND P. STRZELECKI (2019): “Non-base Wage Components as a Source of Wage Adaptability to Shocks: Evidence from European Firms, 2010–2013.” IZA Journal of Labor Policy, 8(1):1–18.

BREWER, M., F. ZILIO, AND T. CROSSLEY (2019): “What Do We Really Know about the Employment Effects of the UK ’ s National Minimum Wage ?”

CARD, D. (1992): “Using Regional Variation in Wages to Measure the Effects of the Federal Minimum Wage.”

CENGIZ, D., A. DUBE, A. LINDNER, AND B. ZIPPERER (2019): “The Effect of Minimum Wages on Low-Wage Jobs: Evidence from the United States Using a Bunching Estimator.”

DOUCOULIAGOS, H. AND T. D. STANLEY (2009): “Publication Selection Bias in Minimumwage Research? A Meta-regression Analysis.” British Journal of Industrial Relations, 47

(2):406–428.

DUSPIVOVÁ, K., J. FISCHER, P. KANTOROVÁ, M. MATEJKAˇ                                             , P. MRÁZEK, M. PROCHÁZKA,

P. SPÁCILˇ , V. SMOLKA, Š. ŠUSTOVÁ, K. VLTAVSKÁ, AND M. ZELENÝ (2013): “Hodnocení vlivu minimální mzdy na sociálne ekonomický vývojˇ CR Certifikovaná metodika.”ˇ Technical report, Prague.

ERIKSSON, T. AND M. PYTLIKOVA (2004): “Firm-level Consequences of Large Minimum-wage Increases in the Czech and Slovak Republics.” Labour, 18(1):75–103.

FIALOVÁ, K. AND M. MYSÍKOVÁ (2009): “The Minimum Wage: Labor Market Consequences in the Czech Republic.” Finance a Uver - Czech Journal of Economics and Finance, 59(3): 255–274.

FRIEDMAN, J. N., T. OLSEN, L. PISTAFERRI, AND R. CHETTY (2011): “Adjustment Costs , Firm Responses , and Micro vs . Macro Labor Supply Elasticities : Evidence from Danish Tax Records.” Quarterly Journal of Economics, 57.

HARASZTOSI, P. AND A. LINDNER (2019): “Who Pays for the Minimum Wage?” American Economic Review, 109(8):2693–2727.

KLEVEN, H. (2016): “Bunching.” The Annual Review of Economics, 435–464.

MACHIN, S., A. MANNING, AND L. RAHMAN (2003): “Where the Minimum Wage Bites Hard: Introduction of Minimum Wages to a Low Wage Sector.” Journal of the European Economic Association, 1(1):154–180.

MEYER, R. AND D. WISE (1983): “The Effects of the Minimum Wage on the Employment and Earnings of Youth.” Journal of Labor Economics, 1(1):289–308.

MINISTRY OF LABOR AND SOCIAL AFFAIRS (2018): “Unemployment Rate.”

MINISTRY OF LABOUR AND SOCIAL AFFAIRS (2018): “The Evolution of the Minimum Wage

since 1991.”

OECD (2018): “Minimum Relative to Average Wages of Full-time Workers.”

OECD (2019): “STAN Industrial Analysis.”

THE CZECH STATISTICAL OFFICE (2017): “Statistical Yearbook of the Czech Republic 2017.” Technical report, Prague.

 

THE CZECH STATISTICAL OFFICE (2019): “Wages, Labor Costs - Time Series.”

THE WORLD BANK GROUP (2019): “GDP Growth (annual %).”

Appendix A:         Wage Measure

Wage measures available in our dataset are based on the total money paid to employees by employers. However, for the purpose of minimum wage analyses, it is necessary to clean the wage data in order to include only the amount of wages that are directly regulated by the minimum wage law^[34]. The monthly wage available in the dataset is defined as

money paid since January 1^st

 monthly wage ⁼ number of months worked since January 1_st                                             (A1)

We strictly follow the minimum wage legislation and adjust the nominator according to the definition of wages in Government Decree No. 89/2012 Sb. We also adjust the number of months worked since January 1^st so as not to include overtime hours. This definition is as close as possible to the definition in the legislation.

Appendix B:         Tables

Table B1: Employees Affected by NMW Increases

year	Number affected by MW in sample	Percent in sample	Fraction in firms with < 100 employees	Mean distance to the new MW level (in CZK)	Median distance to the new MW level (in CZK)
2012	21,659	1.77 %	0.52	890.5 (1331.8)	420.9
2014	10,560	0.85 %	0.54	583.2 (649.2)	427.6
2015	26,548	2.09 %	0.51	738.3 (700.2)	613.7
2016	30,507	2.37 %	0.56	890.1 (744.7)	785.0

* Standard deviations in parenthesis.

Note: The table reports descriptive statistics on employees who were/were not affected by the NMW increases in each of the relevant years. The last two columns report the distances between the existing wage and the NMW level in the next period (among employees affected by NMW increases).

Table B2: Individual Level Characteristics - Percentages of Employees Affected by NMW

Category	2012	2014	2015	2016
Gender Male	1.45	0.69	1.69	1.90
Female	2.22	1.09	2.64	3.00
Age Group <20	4.01	1.36	4.19	3.46
21-30	1.91	0.61	1.97	2.22
31-40	1.73	0.56	1.77	2.00
41-50	1.56	0.87	1.89	2.17
51-60	1.67	1.35	2.57	2.96
>61	3.34	1.63	3.72	3.93
Education Primary	2.84	2.98	4.77	5.42
Apprenticeship	1.81	1.19	2.38	2.85
Secondary	1.46	0.39	1.44	1.66
Third-level	1.52	0.12	1.24	1.41
Post-graduate	1.69	0.06	1.25	1.14
Tenure in the job <1 year	3.57	2.27	4.08	4.17
1-5 years	2.25	1.26	2.95	3.32
>5 years	1.16	0.36	1.18	1.40

Note: The table reports percentages of employees who were exposed to NMW increases in each year (by various characteristics).

Table B3: Occupations: Percentages of Employees Affected in Each Occupational Group and Year

ISCO group	2012	2014	2015	2016
Managers	0.87	0.11	0.80	0.97
Professionals	1.35	0.02	1.11	1.34
Technicians and Associate Professionals	1.16	0.06	0.86	1.01
Clerical Support Workers	1.05	0.20	1.03	1.39
Services and Sales Workers	4.63	3.52	6.98	6.27
Skilled Agricultural, Forestry and Fishery Workers	3.01	0.48	2.12	2.38
Craft and Related Trades Workers	1.24	0.19	1.02	1.33
Plant and Machine Operators and Assemblers	1.40	0.43	1.28	1.66
Elementary Occupations	4.92	6.47	9.10	11.35

Note: The table reports percentages of workers affected by NMW increases in each year and occupational group (2 digit ISCO classification).

Table B4: Industry: Percentages of Employees Affected in Each Industry Group and Year

NACE group	2012	2014	2015	2016
Agric., Forest., Fish.	2.15	0.60	1.78	2.16
Mining and Metalurgy	1.13	0.16	0.50	0.80
Manufacturing	1.13	0.33	1.04	1.27
Utilities	0.45	0.40	0.71	0.84
Construction	1.18	0.24	1.70	1.57
Retail	2.10	0.51	2.90	2.30
Hotels and food service	7.70	4.05	5.37	6.72
Transport	1.49	0.08	0.92	1.22
Banks, insurance	1.14	0.02	0.74	1.03
Real Estate, R&D	6.06	6.41	9.35	10.81
Public Admin., defense	0.39	0.00	1.22	0.64
Education	0.86	0.38	1.49	1.43
Health	1.72	1.94	3.36	5.15
Other Services	3.32	1.43	3.13	4.24
Communications	1.30	0.01	1.22	1.28

Note: The table reports percentages of employees affected by NMW increases in each year and industry (2 digit NACE classification).

Table B5: Job-Cell Characteristics

 2012                                 2014                                 2015                                 2016

 Not affected   Affected   Not affected   Affected   Not affected   Affected    Not affected     Affected

Share	-	0.1870	-	0.3679	-	0.2302	-	0.2532
		(0.214)		(0.319)		(0.261)		(0.287)
Intensity measure	-	0.0078	-	0.0263	-	0.008	-	0.0126
		(0.103)		(0.129)		(0.035)		(0.041)
JC employement	18.3	66.4	22.08	45.2	18.6	64.4	18.5	64.6
	(59.7)	(174.7)	(76.7)	(125.3)	(62.7)	(166.6)	(57.2)	(183.5)
Net hrs worked	1655	1549	1642	1503	1619	1517	1619	1508
	(314)	(404)	(325)	(444)	(342)	(419)	(348)	(431)
Female	0.419	0.521	0.431	0.594	0.425	0.543	0.426	0.532
	(0.39)	(0.36)	(0.39)	(0.36)	(0.39)	(0.36)	(0.39)	(0.36)
Age	41.9	41.3	42	44.3	42.3	41.7	42.3	42.2
	(7.0)	(6.5)	(7.0)	(6.6)	(7.0)	(6.7)	(6.9)	(6.8)
Tenure in the job	9.3	7.4	9.5	5.7	9.7	7.0	9.5	7.1
	(6.8)	(5.5)	(6.7)	(5.9)	(6.8)	(5.1)	(6.7)	(5.71)
Primary educ.	0.043	0.082	0.041	0.180	0.040	0.095	0.040	0.098
	(0.12)	(0.15)	(0.11)	(0.23)	(0.11)	(0.17)	(0.11)	(0.17)
Apprenticeship educ.	0.311	0.360	0.301	0.513	0.295	0.376	0.287	0.369
	(0.34)	(0.32)	(0.33)	(0.30)	(0.33)	(0.32)	(0.33)	(0.32)
Secondary educ.	0.406	0.341	0.406	0.200	0.411	0.319	0.408	0.320
	(0.32)	(0.28)	(0.31)	(0.23)	(0.31)	(0.27)	(0.31)	(0.27)
Tertiary educ.	0.203	0.159	0.215	0.041	0.220	0.153	0.228	0.160
	(0.29)	(0.25)	(0.30)	(0.13)	(0.30)	(0.25)	(0.30)	(0.25)
Czech nationality	0.975	0.957	0.973	0.945	0.973	0.948	0.970	0.943
	(0.09)	(0.11)	(0.09)	(0.16)	(0.09)	(0.13)	(0.09)	(0.14)
N	46,867	5,110	51,491	1,559	47,715	5,507	47,391	6,011

* Standard deviations in parenthesis.

Note: The table reports characteristics of job cells that were/were not exposed to the NMW increases in each year. “Not affected" are the job cells in which all employees were paid above the NMW level effective in the next period. Similarly, “Affected" job cells contain at least one employee paid below the NMW level in the next period.

Table B6: Firm Characteristics

 2012                                 2014                                 2015                                 2016

 Not affected   Affected   Not affected   Affected   Not affected   Affected    Not affected     Affected

Share	-	0.0624	-	0.1154	-	0.0827	-	0.0920
		(0.112)		(0.189)		(0.152)		(0.170)
Intensity measure	-	0.0016	-	0.0059	-	0.0027	-	0.0039
		(0.034)		(0.015)		(0.011)		(0.015)
Firm employment	200.9	459.2	297.4	396.2	208.6	441.4	211.1	440.3
	(328.6)	(1335.2)	(840.9)	(1288.3)	(394.6)	(1262.4)	(358.5)	(1250)
Net hrs worked	1659	1605	1634	1582	1624	1575	1622	1586
	(332)	(367)	(344)	(410)	(358)	(394)	(355)	(392)
Female	0.374	0.444	0.401	0.506	0.386	0.456	0.391	0.455
	(0.25)	(0.26)	(0.25)	(0.27)	(0.26)	(0.25)	(0.25)	(0.26)
Age	41.2	41.2	41.2	42.6	41.7	41.5	41.9	41.5
	(4.6)	(4.7)	(4.8)	(4.7)	(4.7)	(4.7)	(4.8)	(4.6)
Tenure in the job	8.1	7.8	8.2	7.5	8.3	7.6	8.3	7.7
	(5.7)	(5.2)	(5.1)	(6.5)	(4.7)	(4.7)	(4.9)	(5.4)
Primary educ.	0.053	0.071	0.048	0.103	0.048	0.070	0.045	0.070
	(0.097)	(0.105)	(0.079)	(0.154)	(0.086)	(0.113)	(0.081)	(0.112)
Apprenticeship educ.	0.403	0.393	0.363	0.435	0.372	0.378	0.354	0.363
	(0.254)	(0.239)	(0.251)	(0.240)	(0.260)	(0.242)	(0.258)	(0.239)
Secondary educ.	0.340	0.328	0.353	0.303	0.349	0.333	0.351	0.334
	(0.179)	(0.166)	(0.178)	(0.179)	(0.184)	(0.172)	(0.182)	(0.175)
Tertiary educ.	0.162	0.156	0.193	0.108	0.194	0.167	0.202	0.180
	(0.191)	(0.182)	(0.209)	(0.134)	(0.213)	(0.189)	(0.219)	(0.201)
Czech nationality	0.967	0.956	0.958	0.945	0.963	0.945	0.957	0.940
	(0.075)	(0.094)	(0.088)	(0.148)	(0.083)	(0.118)	(0.092)	(0.121)
N	1,775	1,880	3,253	662	1,903	1,968	1,717	2,100

Standard deviations in parentheses.

Note:The table reports characteristics of firms that were/were not exposed to the NMW increases in each year. “Not affected" are firms in which all employees were paid above the NMW level effective in the next period. Similarly, “Affected" firms contain at least one employee paid below the NMW level in the next period.

Table B7: Employment Effects of NMW Increase: 2012-2014 Data, Firm Level

		All firms		Firms with > 100 employees
	Share	Gap	Weighted	Share	Gap	Weighted
Share	-0.248**		-0.241*	-0.189		-0.240*
	(0.113)		(0.126)	(0.136)		(0.134)
Gap		0.0427			0.0506
		(0.107)			(0.103)
Age	0.0191	0.0194	0.0653***	0.0567*	0.0570*	0.0742***
	(0.0283)	(0.0284)	(0.0250)	(0.0302)	(0.0303)	(0.0278)
Age sq.	-0.0287	-0.0298	-0.0855***	-0.0718**	-0.0731**	-0.0951***
	(0.0349)	(0.0350)	(0.0296)	(0.0354)	(0.0357)	(0.0330)
Tenure in the job	-0.00422	-0.00388	-0.0120**	-0.0180**	-0.0171**	-0.0205***
	(0.00257)	(0.00257)	(0.00576)	(0.00735)	(0.00732)	(0.00637)
Tenure sq.	0.000138***	0.000140***	0.000508**	0.000761**	0.000743**	0.000866***
	(0.0000308)	(0.0000305)	(0.000220)	(0.000316)	(0.000316)	(0.000242)
Female	0.00733	0.000303	0.0502	0.0397	0.0361	0.0494
	(0.0464)	(0.0454)	(0.0436)	(0.0589)	(0.0583)	(0.0470)
Czech	0.0304	0.0640	0.117	0.0961	0.126	0.129
	(0.129)	(0.131)	(0.108)	(0.116)	(0.121)	(0.113)
Constant	-0.193	-0.237	-1.153**	-1.170*	-1.195*	-1.391**
	(0.629)	(0.628)	(0.507)	(0.612)	(0.617)	(0.550)
Educ. cat.	Yes	Yes	Yes	Yes	Yes	Yes
Firm size	Yes	Yes	Yes	Yes	Yes	Yes
Industry	Yes	Yes	Yes	Yes	Yes	Yes
County	Yes	Yes	Yes	Yes	Yes	Yes
Occupation	Yes	Yes	Yes	Yes	Yes	Yes
Observations	2,206	2,206	2,206	1,605	1,605	1,605
Adjusted R2	0.082	0.077	0.198	0.079	0.076	0.187

Standard errors in parentheses; * p<0.10, ** p<0.05, *** p<0.010

Note: The table reports the employment effects (Dep. var: ? logEmpl) of the NMW increase in 2013 using firm-level data from 2012 and 2014. The columns represent different exposure measures. Columns (1)-(3) consider all firms; columns (4)-(6) consider only firms that have more than 100 employees.

Table B8: Employment Effects of NMW Increases: 2012-2014 Data, All Job Cells from the Manufacturing Industry

		All cells			Cells > 10
	Share	Gap	Weighted	Share	Gap	Weighted
Share	-0.269***		-0.112	-0.212		-0.0631
	(0.103)		(0.163)	(0.179)		(0.180)
Gap		-1.252***			-0.942***
		(0.128)			(0.166)
Age	0.0269***	0.0270***	0.0749***	0.0573***	0.0578***	0.0976***
	(0.00757)	(0.00755)	(0.0213)	(0.0170)	(0.0169)	(0.0288)
Age sq.	-0.0326***	-0.0327***	-0.0977***	-0.0765***	-0.0771***	-0.129***
	(0.00875)	(0.00873)	(0.0259)	(0.0204)	(0.0203)	(0.0355)
Tenure in the job	-0.0144***	-0.0142***	-0.0140**	-0.0144***	-0.0141***	-0.0155**
	(0.00266)	(0.00266)	(0.00582)	(0.00523)	(0.00525)	(0.00749)
Tenure sq.	0.000446***	0.000443***	0.000704***	0.000611***	0.000603***	0.000848***
	(0.0000757)	(0.0000756)	(0.000194)	(0.000175)	(0.000175)	(0.000266)
Female	-0.0252	-0.0253	-0.138**	-0.0216	-0.0218	-0.137**
	(0.0184)	(0.0185)	(0.0574)	(0.0327)	(0.0326)	(0.0623)
Czech	-0.0340	-0.0312	-0.0521	0.161*	0.164*	-0.0343
	(0.0666)	(0.0668)	(0.143)	(0.0948)	(0.0946)	(0.161)
Constant	-0.543***	-0.550***	-2.180***	-1.815***	-1.826***	-3.213***
	(0.173)	(0.173)	(0.649)	(0.364)	(0.364)	(0.820)
Educ. cat.	Yes	Yes	Yes	Yes	Yes	Yes
Firm size	Yes	Yes	Yes	Yes	Yes	Yes
Industry	Yes	Yes	Yes	Yes	Yes	Yes
County	Yes	Yes	Yes	Yes	Yes	Yes
Occupation	Yes	Yes	Yes	Yes	Yes	Yes
Observations	10,819	10,819	10,819	5,438	5,438	5,438
Adjusted R2	0.039	0.038	0.212	0.061	0.061	0.224

Standard errors in parentheses; * p<0.10, ** p<0.05, *** p<0.010.

Note: The table reports the employment effects (Dep. var: ? logEmpl) of the 2013 NMW increase estimated on the job cells that belong to the Manufacturing industry. We use data from 2012 and 2014. Columns represent different exposure measures. The columns (1)-(3) consider all job cells; columns (4)-(6) consider only job cells with more than 10 employees.

Table B9: Employment Effects - Interactions with Local Unemployment Rates

 All cells                                  Cells > 10

 Share                Gap               Share                Gap

2012
Share	-0.181		-0.558
	(0.225)		(0.373)
Shr*Unempl	0.00803		0.0456
	(0.0218)		(0.0385)
Gap		0.127		-1.846
		(1.691)		(2.694)
Gap * Unempl		-0.0391		0.217
		(0.180)		(0.287)
Unemployment	0.00311	0.00377	0.00580	0.00778
	(0.00898)	(0.00909)	(0.0128)	(0.0130)
2014
Share	-0.0798		0.00313
	(0.152)		(0.224)
Shr*Unempl	0.0121		0.00743
	(0.0143)		(0.0261)
Gap		-0.505		5.281**
		(1.170)		(2.157)
Gap * Unempl		0.165		-0.479*
		(0.171)		(0.278)
Unemployment	-0.0000338	-0.0000157	-0.0103	-0.00668
	(0.00610)	(0.00590)	(0.0136)	(0.00744)
2015
Share	-0.0519		-0.0490
	(0.0876)		(0.122)
Shr*Unempl	0.00620		0.00211
	(0.0107)		(0.0151)
Gap		-0.402		1.107
		(0.344)		(2.120)
Gap * Unempl		0.0642		-0.0491
		(0.0598)		(0.265)
Unemployment	0.0128***	0.0130***	0.0200***	0.0203***
	(0.00423)	(0.00419)	(0.00692)	(0.00683)
2016
Share	-0.0290		-0.276**
	(0.0644)		(0.122)
Shr*Unempl	-0.00136		0.0212
	(0.00881)		(0.0137)
Gap		0.901		-5.264**
		(0.585)		(2.509)
Gap * Unempl		-0.253*		0.407*
		(0.154)		(0.233)
Unemployment	-0.000322	0.000557	-0.00168	-0.00157
	(0.00440)	(0.00430)	(0.00723)	(0.00717)
Controls	Yes	Yes	Yes	Yes

Standard errors in parentheses; * p<0.10, ** p<0.05, *** p<0.010.

Note: The table reports employment effects (Dep. var: ? logEmpl) using the interactions of exposure measures and county-specific unemployment rates in each year, i.e., we ask whether the employment effect is stronger in counties experiencing high unemployment rates. Columns represent different exposure measures. The columns (1)-(2) consider all job cells from the 1st quartile of job-cell wage distribution; columns (3)-(4) consider only job cells from the 1st quartile that consist of more than 10 employees. We control for age, age sq., tenure in the job, tenure sq., county, firm size, and shares of females, Czechs and workers by highest level of educational attainment,

Table B10: Employment Effects with Job-Cell Fixed Effects

                                                                          ? logEmpl                                                          ? logWage

 (1)                                     (2)                                       (1)                               (2)

Share	-0.0572***		0.105***
	(0.0194)		(0.00825)
Gap		-0.471**		0.584***
		(0.228)		(0.0969)
Age	-0.0277***	-0.0276***	0.00000390	-0.000328
	(0.00487)	(0.00487)	(0.00167)	(0.00167)
Age sq.	0.0285***	0.0282***	0.00575***	0.00626***
	(0.00589)	(0.00589)	(0.00200)	(0.00201)
Tenure in the job	-0.0307***	-0.0307***	0.00627***	0.00635***
	(0.00206)	(0.00206)	(0.000747)	(0.000750)
Tenure sq.	0.000297***	0.000297***	-0.0000689***	-0.0000688***
	(0.0000237)	(0.0000237)	(0.0000144)	(0.0000142)
Female	0.0635*	0.0640*	-0.0738***	-0.0743***
	(0.0375)	(0.0375)	(0.0106)	(0.0106)
Czech nat.	-0.0984	-0.0976	-0.146***	-0.146***
	(0.0607)	(0.0608)	(0.0198)	(0.0199)
Constant	2.542***	2.530***	9.527***	9.647***
	(0.153)	(0.154)	(0.0445)	(0.0785)
Educ. cat.	Yes	Yes	Yes	Yes
Firm size	Yes	Yes	Yes	Yes
Industry	Yes	Yes	No	Yes
Observations	60,441	60,441	60,441	60,441
Adjusted R2	0.053	0.053	0.067	0.062

Standard errors in parentheses; * p<0.10, ** p<0.05, *** p<0.010.

Note: The table reports the employment and wage effects (Dep. var: ? logEmpl, ? logWage) of the NMW increases. We estimate linear regressions on job-cell panel data for 2012-2017. The job-cell fixed effects are included. The first two rows are our coefficients of interest. We use all job cells.

Table B11: Employment Effects: One Large Artificial NMW Increase Between 2012-2017

		All cells			Cells > 10
	Share	Gap	Weighted	Share	Gap	Weighted
Share	-0.0414		-0.0740	-0.0529		-0.0480
	(0.0300)		(0.0869)	(0.0602)		(0.103)
Gap		0.116			0.121
		(0.132)			(0.165)
Age	0.0185***	0.0185***	0.0668***	0.0346***	0.0346***	0.0881***
	(0.00466)	(0.00465)	(0.0210)	(0.0125)	(0.0125)	(0.0292)
Age sq.	-0.0238***	-0.0239***	-0.0875***	-0.0526***	-0.0528***	-0.119***
	(0.00538)	(0.00538)	(0.0244)	(0.0147)	(0.0147)	(0.0346)
Tenure in the job	-0.0114***	-0.0113***	0.00249	0.00200	0.00228	0.0105
	(0.00280)	(0.00278)	(0.00509)	(0.00401)	(0.00401)	(0.00695)
Tenure sq.	0.000341***	0.000340***	0.000104	0.0000567	0.0000507	-0.000101
	(0.0000993)	(0.0000985)	(0.000160)	(0.000131)	(0.000131)	(0.000232)
Female	-0.0562***	-0.0569***	-0.226***	-0.0693***	-0.0708***	-0.235***
	(0.0121)	(0.0121)	(0.0573)	(0.0263)	(0.0263)	(0.0661)
Czech	0.0345	0.0368	-0.0335	0.0181	0.0247	-0.0523
	(0.0466)	(0.0466)	(0.132)	(0.0930)	(0.0934)	(0.153)
Constant	-0.383***	-0.390***	-1.347***	-0.884***	-0.892***	-1.759***
	(0.112)	(0.112)	(0.479)	(0.330)	(0.330)	(0.665)
Educ. cat.	Yes	Yes	Yes	Yes	Yes	Yes
Firm size	Yes	Yes	Yes	Yes	Yes	Yes
Industry	Yes	Yes	Yes	Yes	Yes	Yes
County	Yes	Yes	Yes	Yes	Yes	Yes
Occupation	Yes	Yes	Yes	Yes	Yes	Yes
Observations	34,002	34,002	34,002	14,401	14,401	14,401
Adjusted R2	0.030	0.030	0.147	0.056	0.055	0.166

Standard errors in parentheses; * p<0.10, ** p<0.05, *** p<0.010.

Note: The table reports the employment effects (Dep. var: ? logEmpl) of an artificial increase in the NMW between 2012 and 2017. We use all job cells that survived from 2012 to 2017. Columns represent different exposure measures. The columns (1)-(3) consider all job cells; columns (4)-(6) consider only job cells that consist more than 10 employees.

Table B12: Wage Effects: One Large Artificial NMW Increase Between 2012-2017

		All cells			Cells > 10
	Share	Gap	Weighted	Share	Gap	Weighted
Share	0.0893***		0.0644***	0.0744***		0.0566**
	(0.0108)		(0.0239)	(0.0183)		(0.0274)
Gap		0.286			0.111
		(0.179)			(0.165)
Age	-0.0140***	-0.0142***	-0.0301***	-0.0197***	-0.0200***	-0.0385***
	(0.00166)	(0.00166)	(0.00685)	(0.00322)	(0.00322)	(0.00931)
Age sq.	0.0142***	0.0143***	0.0332***	0.0215***	0.0219***	0.0435***
	(0.00197)	(0.00197)	(0.00760)	(0.00382)	(0.00382)	(0.0105)
Tenure in the job	-0.00247***	-0.00252***	-0.00315***	-0.00237**	-0.00259***	-0.00369**
	(0.000487)	(0.000491)	(0.00112)	(0.000983)	(0.000985)	(0.00147)
Tenure sq.	0.0000323**	0.0000323**	0.0000786**	0.0000499	0.0000538*	0.000110**
	(0.0000133)	(0.0000135)	(0.0000327)	(0.0000309)	(0.0000310)	(0.0000453)
Female	0.0464***	0.0473***	0.0622***	0.0524***	0.0540***	0.0661***
	(0.00427)	(0.00427)	(0.00800)	(0.00619)	(0.00617)	(0.00946)
Czech	0.0348*	0.0362**	-0.0146	-0.0128	-0.0134	-0.0175
	(0.0181)	(0.0182)	(0.0259)	(0.0246)	(0.0248)	(0.0294)
Constant	0.495***	0.498***	0.878***	0.543***	0.548***	0.985***
	(0.0489)	(0.0489)	(0.150)	(0.152)	(0.152)	(0.229)
Educ. cat.	Yes	Yes	Yes	Yes	Yes	Yes
Firm size	Yes	Yes	Yes	Yes	Yes	Yes
Industry	Yes	Yes	Yes	Yes	Yes	Yes
County	Yes	Yes	Yes	Yes	Yes	Yes
Occupation	Yes	Yes	Yes	Yes	Yes	Yes
Observations	34,002	34,002	34,002	14,401	14,401	14,401
Adjusted R2	0.085	0.084	0.186	0.124	0.122	0.215

Standard errors in parentheses; * p<0.10, ** p<0.05, *** p<0.010.

Note: The table reports the wage effects (Dep. var: ? logCellWage) of an artificial increase in the NMW between 2012 and 2017. We use only job cells that survived from 2012 to 2017. Columns represent different exposure measures. The columns (1)-(3) consider all job cells; columns (4)-(6) consider only job cells that consist of more than 10 employees.

Table B13: Employment Effects for Low- and High-Wage Employees: Firm-Level Exposure

? log Employment

 low-paid employees    high-paid employees

 2013 NMW increase                    0.007                                    0.002

 (0.025)                                 (0.007)

2015 NMW increase     0.007     0.010*

 (0.005)                                 (0.005)

2016 NMW increase     -0.002   0.004

 (0.003)                                 (0.004)

2017 NMW increase     0.011     0.004

 (0.012)                                 (0.004)

Note: The table reports the Share estimates from regression equations where the dependent variables are ?logEmpl (firm level) and independent variables are the Share measures at the firm level during 2013-2017. The employment changes include only employees who belong to the first quartile of the job-cell wage distribution in the first column and employees from the 2nd-4th quartile in the second column. Rows show estimated effects for different NMW increases. At the firm level, we control for age, age sq., tenure in the job, tenure sq., county, firm size, industry, and shares of females, Czechs, and the highest level of educational attainment, and they are the same for both subsamples; Standard errors in parenthesis, p-values * p<0.10, ** p<0.05, *** p<0.010.

Table B14: Wage Effects for Different Subsamples of Job Cells

	All observations	Below median	1st quartile	10 most affected occ
2012
Share	0.0359**	0.0646***	0.0733***	0.0496**
2014	(0.0174)	(0.0190)	(0.0218)	(0.0204)
Share	0.0906***	0.0916***	0.0874***	0.0714***
2015	(0.0284)	(0.0286)	(0.0293)	(0.0205)
Share	0.0215**	0.0245***	0.0280***	0.0464***
2016	(0.00935)	(0.00859)	(0.00792)	(0.0108)
Share	0.0481***	0.0577***	0.0491***	0.0443***
	(0.00874)	(0.00852)	(0.00748)	(0.00895)
Controls	Yes	Yes	Yes	Yes

Standard errors in parentheses; * p<0.10, ** p<0.05, *** p<0.010.

Note: The table reports ß₃ coefficients from Eq. 4 for various subsamples of job cells based on the job-cell wage distribution in each year. We control for age, age sq., tenure in the job, tenure sq., county, firm size, and shares of females, Czechs, and the highest level of educational attainment.

Table B15: Wage Cyclicality in Firms with Low-Paid Employees

	Low-paid: 1st decile	Low-paid: 1st quartile	Low-paid: below median
Pcnt. change in ind. prod.	0.000798***	0.000501**	-0.000386
	(0.000177)	(0.000234)	(0.000386)
Share of low-paid	0.602***	0.579***	0.632***
	(0.0298)	(0.0204)	(0.0204)
Ind. growth*shr of low-paid	-0.00215***	-0.000625	0.000829
	(0.000757)	(0.000503)	(0.000539)
Adjusted R2	0.170	0.238	0.278

Standard errors in parentheses; * p<0.10, ** p<0.05, *** p<0.010.

Note: The table reports results on wage cyclicality of firms with varying proportions of low-paid employees across the economic cycle. The dependent variable is ?logWage. The percentage change in industrial production approximates the phase of the economic cycle. We are primarily interested in the estimated coefficients “Ind. growth*shr of low-paid", which refers to the interaction of the growth in a particular industry and the share of low-paid employees. These estimates allow us to determine whether wage growth in firms with/without higher shares of low-paid employees systematically differs during economic booms and busts. The columns represent different measures of low-paid employees. We control for age, age sq., tenure in the job, tenure sq., county, firm size, and shares of females, Czechs, and the highest level of educational attainment. We use semiannual data from SES 2007-2012, all firms. The regressions contains firm fixed effects.

Table B16: Employment Cyclicality in Firms with Low-Paid Employees

	Low-paid: 1st decile	Low-paid: 1st quartile	Low-paid: below median
Pcnt. change in ind. prod.	0.00117***	0.00113**	0.00182**
	(0.000403)	(0.000489)	(0.000711)
Share of low-paid	0.0662	-0.0896	-0.129***
	(0.0801)	(0.0602)	(0.0492)
Ind. growth*shr of low-paid	0.00113	0.000967	-0.000499
	(0.00273)	(0.00142)	(0.00114)
Constant	-1.349**	-1.392**	-1.327*
	(0.683)	(0.677)	(0.687)
Controls	Yes	Yes	Yes
Observations	11,130	11,130	11,130
Adjusted R2	0.101	0.101	0.102

Standard errors in parentheses; * p<0.10, ** p<0.05, *** p<0.010.

Note: The table reports results on employment cyclicality of firms with varying proportions of low-paid employees across the economic cycle. The dependent variable is ?logEmpl. The percentage change in industrial production approximates the phase of the economic cycle. We are primarily interested in the estimated coefficients “Ind. growth*shr of low-paid", which refers to the interaction of the growth in a particular industry and the share of low-paid employees. These estimates allow us to determine whether the employment patterns in firms with/without higher shares of low-paid employees systematically differ during economic booms and busts. The columns represent different measures of low-paid employees. We control for age, age sq., tenure in the job, tenure sq., county, firm size, and shares of females, Czechs, and the highest level of educational attainment. We use semiannual data from SES 2007-2012. The regressions contains firm fixed effects.

 

CNB Working Paper Series (since 2020) 

WP 2/2021          Jakub Grossmann The effects of minimum wage increases in the Czech Republic

WP 1/2021         Martin Časta            Deriving equity risk premium using dividend futures

WP 15/2020	Petr Polák Nikol Poláková Anna Tlustá	How bad are trade wars? Evidence from tariffs
WP 14/2020	Dominika Ehrenbergerová Josef Bajzík	The effect of monetary policy on house prices – How strong is the transmission?
WP 13/2020	Zuzana Rakovská	Composite survey sentiment as a predictor of future market returns: Evidence for German equity indices
WP 12/2020	Vojtěch Siuda	A top-down stress-testing framework for the nonfinancial corporate sector
WP 11/2020	Hana Hejlová Michal Hlaváček Blanka Vačkova	Estimating commercial property price misalignment in the CEE countries
WP 10/2020	Zuzana Rakovská Dominika Ehrenbergerová Martin Hodula	The power of sentiment: Irrational beliefs of households and consumer loan dynamics
WP 9/2020	Ivan Sutóris	The intertemporal cost of living and dynamic inflation: The case of the Czech Republic
WP 8/2020	Martin Hodula Jan Janků Martin Časta Adam Kučera	On the determinants of life and non-life insurance premiums
WP 7/2020	František Brázdik Tibor Hlédik Zuzana Humplová Iva Martonosi Karel Musil  Jakub Ryšánek Tomáš Šestořád Jaromír Tonner Stanislav Tvrz Jan Žáček	The g3+ model: An upgrade of the Czech National Bank’s core forecasting framework
WP 6/2020	Volha Audzei Jan Brůha	A model of the Euro Area, China and the United States: Trade links and trade wars
WP 5/2020	Dominika Ehrenbergerová Martin Hodula Zuzana Rakovská	Does capital-based regulation affect bank pricing policy?
WP 4/2020	Alexis Derviz	Sovereign capital, external balance, and the investment-based

WP 3/2020       Milan Szabo

Balassa-Samuelson effect in a global dynamic equilibrium

Growth-at-risk: Bayesian approach

 

WP 2/2020	Martin Hodula  Ngoc Anh Ngo	Finance, growth and (macro)prudential policy: European evidence
WP 1/2020	Michal Franta Ivan Sutóris	Dynamics of Czech inflation: The role of the trend and the cycle

 

 

 

CNB Research and Policy Notes (since 2020) 

RPN 3/2020	Simona Malovaná Martin Hodula  Zuzana Rakovská	Researching the research: A central banking edition
RPN 2/2020	Simona Malovaná Josef Bajzík Dominika Ehrenbergerová Jan Janků	A prolonged period of low interest rates: Unintended consequences
RPN 1/2020	Simona Malovaná	How to organize research in central banks: The Czech National Bank's experience

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

CZECH NATIONAL BANK

Na Příkopě 28

115 03 Praha 1

Czech Republic

 

ECONOMIC RESEARCH DIVISION

Tel.: +420 224 412 321 Fax: +420 224 412 329 http://www.cnb.cz 

e-mail: research@cnb.cz

 

ISSN 1803-7070 

www.cnb.cz

 

---